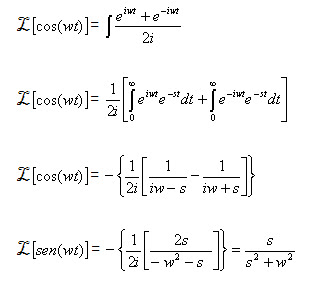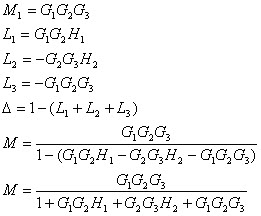SIMULACION Y CONTROL DE PROCESOS UDENAR

Un sistema de control puede tener varios componentes. Para mostrar las funciones que lleva a cabo cada componente en la ingeniería de control, por lo general se usa una representación denominada diagrama de bloques.

Un diagrama de bloques de un sistema es una representación gráfica de las funciones que lleva a cabo cada componente. Tal diagrama muestra las relaciones existentes entre los diversos componentes.

En un diagrama de bloques se enlazan una con otra todas las variables del sistema, mediante bloques funcionales. El bloque funcional o simplemente bloque es un símbolo para representar la operación matemática que sobre la señal de entrada hace el bloque para producir la salida.

La figura muestra un elemento del diagrama de bloques. La punta de flecha que señala el bloque indica la entrada, y la punta de flecha que se aleja del bloque representa la salida. Tales flechas se conocen como señales.

Observe que las dimensiones de la señal de salida del bloque son las dimensiones de la señal de entrada multiplicadas por las dimensiones de la función de transferencia en el bloque.

Un diagrama de bloques contiene información relacionada con el comportamiento dinámico, pero no incluye información de la construcción física del sistema. En consecuencia, muchos sistemas diferentes y no relacionados pueden representarse mediante el mismo diagrama de bloques.

REDUCCIÓN DE UN DIAGRAMA DE BLOQUES

Es importante señalar que los bloques pueden conectarse en serie, sólo si la entrada de un bloque no se ve afectada por el bloque siguiente. Si hay efectos de carga entre los componentes, es necesario combinarlos en un bloque único.

Un diagrama de bloques complicado que contenga muchos lazos de realimentación se simplifica mediante un reordenamiento paso a paso mediante las reglas del álgebra de los diagramas de bloques. Algunas de estas reglas importantes aparecen en la tabla y se obtienen escribiendo la misma ecuación en formas distintas.

La simplificación de un diagrama de bloques mediante reordenamientos y sustituciones reduce de manera considerable la labor necesaria para el análisis matemático subsecuente. Sin embargo, debe señalarse que, conforme se simplifica el diagrama de bloques, las funciones de transferencia de los bloques nuevos se vuelven más complejas, debido a que se generan polos y ceros nuevos.

REGLAS DE ALGEBRA PARA BOQLES

Al simplificar un diagrama de bloques, recuerde lo siguiente:

1. El producto de las funciones de transferencia en la dirección de la trayectoria directa debe ser el mismo.

2. El producto de las funciones de transferencia alrededor del lazo debe ser el mismo.

Estabilidad de Sistemas Dinámicos

La estabilidad (asociada a conceptos relacionados con la respuesta dinámica de un sistema) es una propiedad fundamental de los sistemas de control, tan importante como la robustez, el rendimiento y otras características que lo identifican.

El análisis de estabilidad de los sistemas no lineales es un problema complejo donde no existe una técnica común que pueda resolver todos los casos que se presentan. Al mecanismo de modelado se le exigen altas prestaciones, puesto que las técnicas de estabilidad en tiempo continuo están más desarrolladas y extendidas que el análisis en tiempo discreto, por lo que la incorporación de retrasos en las variables de control y salida de la planta, que mejoran el modelo, no se pueden realizar.

Teoría de Lyapunov

Es la más generalizada de las herramientas para el estudio de la estabilidad de sistemas. Esta teoría estábasada en el trabajo “El problema general de la estabilidad del movimiento” del matemático ruso Alexandr Mikhailovich Lyapunov publicado en 1892. La potencia de este método es su generalización, puede aplicarse a sistemas tanto variantes en tiempo (sistemas no autónomos) como invariantes en tiempo (sistemas autónomos), independiente del orden del sistema.

Existen dos métodos fundamentales de análisis:

· Método indirecto: Presupone que la estabilidad de un sistema no lineal próximo a un punto de equilibrio es aproximado a un sistema equivalente linealizado, lo cual constituye una justificación teórica para el uso del control lineal como método aplicable a plantas inherentemente no lineales.

Utiliza la linealización de un sistema para determinar la estabilidad local en un punto de equilibrio. Para un sistema no lineal de la forma:

𝐱 = 𝐟(𝐱)

El resultado de linealizar alrededor del punto de equilibrio en el origen del espacio de estados x = 0, utilizando los primeros términos del desarrollo de la serie de Taylor, es:

Si se evalúa el Jacobiano J en el punto de equilibrio x = 0 (en el caso de que el punto de equilibrio x = x^esea diferente de cero se puede cambiar el punto de equilibrio al origen) y los autovalores de la matriz resultante tienen parte real negativa, entonces se cumple una condición necesaria y suficiente para afirmar que el punto de equilibrio del sistema es asintóticamente estable. Nótese que la anterior aseveración es válida sólo para el punto de equilibrio y un espacio de estados alrededor del mismo no muy lejano.

Ejemplo:

Suponga el siguiente sistema:

Las derivadas con respecto a las variables de estado cumplen

por lo que el sistema resulta

Finalmente, al evaluar en el punto de equilibrio x = 0, se tiene que el sistema linealizado equivalente es

A continuación se muestran algunos comportamientos de sistemas dinámicos (gráficos generados por el programa pphase7) y los autovalores de las matrices.

· Método directo: Es una generalización de los conceptos de energía asociados a un sistema mecánico: el movimiento de un sistema mecánico es estable si la energía mecánica total decrece con el tiempo. Basado en lo anterior, para determinado sistema se define una función que se supone describe su energía (función de Lyapunov) y se analiza si esta decrece.

Se basa en la representación matemática de un principio físico: si la energía de un sistema se disipa de forma continuada, entonces el sistema debe converger a un punto de equilibrio de dicho sistema. La formulación matemática se fundamenta en la búsqueda de una función de Lyapunov que pueda caracterizar el comportamiento del sistema dinámico bajo estudio.

La siguiente figura representa a un sistema que muestra un comportamiento estable

Este es el método más general para determinar la estabilidad de sistemas no lineales y/o variantes con el tiempo. Contrario al método indirecto de Lyapunov, este método no requiere de la solución explícita de las ecuaciones diferenciales para el análisis; es decir, se determina la estabilidad del sistema sin resolver las ecuaciones de estado. Esto ofrece una gran ventaja porque, por lo general, es muy difícil despejar las ecuaciones de estado no lineales y/o variantes con el tiempo.

LOS CONTROLADORES PID

SISTEMA DE CONTROL

Es el conjunto de dispositivos que colaboran en la realización de una tarea, donde el principio básico del control es la regulación automática o guía de sistemas dinámicos o dispositivos bajo

condiciones de estados estacionarios y transitorios. El uso efectivo de estos resultados depende de varios factores como lo son:

La realimentación; lo cual hace posible el establecimiento y mantenimiento de estabilidad en la operación del sistema.

La disminución de la sensibilidad de funcionamiento; para limitaciones de diseño, para variaciones de los parámetros de la planta y no linealidades de la planta

La adaptación del comportamiento del sistema a las características desconocidas o variables con el tiempo.

Sus aplicaciones son muy diversas pero es esencial en el control numérico de las maquinas herramientas, industrias de manufactura, industria aeroespacial, diseño en la industria automotriz además en las operaciones industriales como el control de presión, temperatura, humedad, viscosidad y flujo en la industria de proceso.

COMPONENTES BASICOS SISTEMA DE CONTROL

Un sistema de control básicamente está compuesto por:

1. Objetivos de control

2. Componentes del sistema de control

3. Resultados o Salidas

Según como se muestra en la figura

DEFINICIONES B´ASICAS

Variable Controlada y Manipulada: La variable controlada es la cantidad o condición que se mide y se controla, y la manipulada es la cantidad o condición que el controlador modifica para afectar el valor de la variable controlada.

Perturbación: señal que tiende a afectar negativamente el valor de la salida del sistema.

Control Realimentado: se refiere a una operación que en presencia de perturbaciones tiende a reducir la diferencia entre la salida de un sistema y la entrada de referencia siendo esto de manera continua con base a esta referencia.

SISTEMAS DE CONTROL EN LAZO ABIERTO-LAZO CERRADO

Sistemas en Lazo Abierto

Son sistemas en los cuales la salida no tiene efecto sobre la señal de control, es decir, no se mide

la salida en estos sistemas ni se realimenta para comparar con la entrada. En estos sistemas, la precisión depende de la calibración y la presencia de perturbaciones. Un esquema de este tipo s

Presenta en la figura

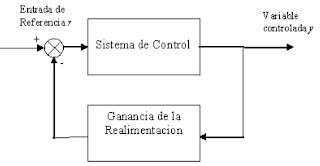
Sistemas en Lazo Cerrado o Realimentados

Es un sistema que mantiene una relación preestablecida entre la salida y la entrada de referencia comparándola y usando la referencia como medio de control. En estos sistemas se alimenta al controlador con la señal de error de actuación, la cual es la diferencia entre la entrada y la señal de realimentación a fin de reducir el error y llevar la salida del sistema a un valor conveniente. Su Representación es la que muestra en la figura

COMPARACI´ON ENTRE SISTEMAS EN LAZO ABIERTO Y LAZO CERRADO

Lazo Abierto

La estabilidad del sistema no es un problema importante en este tipo de sistemas y es más fácil de lograr Son aplicables cuando se conoce con anticipación las entradas y no existen perturbaciones Se usan componentes relativamente precisos y baratos para obtener el control adecuado.

Lazo Cerrado

La estabilidad es una función principal en este tipo de sistema ya que puede conducir a corregir exceso de errores que producen oscilaciones de amplitud constante y cambiante Son aplicables cuando se presentan perturbaciones y/o impredecibles en los componentes del sistema Emplea mayor cantidad de componentes siendo estos más precisos y por ende más costosos. La realimentación vuelve la respuesta insensible a las perturbaciones externas y variaciones internas en los parámetros del sistema Una combinación adecuada entre controles de lazo abierto y cerrado es menos costosa y ofrecer ´a un desempeño satisfactorio del sistema general.

AN´ALISIS EN EL DOMINIO DEL TIEMPO

El análisis en el dominio del tiempo se relaciona con el estudio de la respuesta de los sistemas a la señales aperiódicas tales como: entrada escalón, rampa, parábola e impulso.

Respuesta Transitoria y Respuesta en Estado Estable

La respuesta en el tiempo en un sistema de control consta de dos partes: la respuesta transitoria y la respuesta en estado estable. Se entiende por régimen transitorio a la respuesta que va del Estado inicial al estado final; y por régimen permanente a la manera en la cual se comporta la Salida del sistema conforme el tiempo (t) tiende a infinito.

Sistemas de Primer Orden

Un típico sistema de primer orden está representado físicamente por un circuito RC, un sistema térmico o algo similar, su relación entrada salida se obtiene mediante:

su representación en diagrama de bloques es el mostrado en la figura

En la siguiente figura se muestra un análisis de la respuesta del sistema de entrada escalón, e impulso unitario.

Sistemas de Segundo Orden

La función de transferencia prototipo de un sistema de segundo orden en lazo cerrado es:

su representación en diagrama de bloques es la mostrada en la figura:

El comportamiento dinámico de un sistema de segundo orden se describe en términos de los parámetros _ y ln,en base a esto se clasifica el sistema de la siguiente manera:

1. Caso Sub amortiguado 0< _ < 1

2. Caso Críticamente amortiguado _ = 1

3. Caso Sobre amortiguado _ > 1

A continuación se muestra en la figura la respuesta típica al escalón unitario de un sistema de segundo orden. donde:

Tiempo de Retardo td: es el tiempo requerido para que la respuesta alcance la primera vez la mitad del valor final.

Tiempo de Levantamiento tr: es el tiempo requerido para que la respuesta pase del 10 al 90 por ciento, del 5 al 95 por ciento o del 0 al 100 por ciento de su valor final. Para sistemas sub amortiguados suele usarse un tiempo de levantamiento de 0 a 100 por ciento; y para sistemas

Sobre amortiguados 10 a 90 por ciento.

Tiempo Pico tp: es el tiempo requerido para que la respuesta alcance el primer pico del sobrepaso.

Sobrepaso máximo Mp: es el valor pico máximo de la curva de respuesta medido a partir de la unidad. Si el valor final en estado estable de la respuesta es diferente de la unidad, es común usar el porcentaje de sobre paso máximo.

Tiempo de Asentamiento Ts: es el tiempo que se requiere para que la curva de respuesta alcance un rango alrededor del valor final del tamaño especificado por el porcentaje absoluto del valor final y permanezca dentro de el.

ANALISIS EN EL DOMINIO DEL LA FRECUENCIA

Se conoce con el termino respuesta en frecuencia a la respuesta de un sistema en estado estable a una entrada senoidal. En los métodos de la respuesta en frecuencia, la frecuencia de la señal de entrada se varía en un cierto rango para estudiar la respuesta resultante. El interés de tratar

Entradas sinusoidales esta en que la respuesta del sistema a estas señales contiene información sobre la respuesta a señales más generales. La salida en estado estable para una entrada senoidal viene dada por el sistema:

La entrada r(t) es senoidal y se obtiene mediante:

si el sistema estable la salida c(t) se obtiene a partir de:

Su representación en diagrama de bloques es la mostrada en la figura

Representación Grafica de las Características de la Respuesta en Frecuencia

La función de transferencia senoidal, función compleja de la frecuencia se caracteriza por su magnitud y ´Angulo de fase, con la frecuencia como parámetro. Por lo general se usan representaciones graficas de las funciones de transferencias senoidales:

1. Trazas de Bode o Trazas Logarítmicas

2. Traza de Nyquist o Traza Polar

3. Traza de Magnitud Logarítmica contra la Fase

4.2 Trazas de Bode

Los diagramas de Bode consisten de un par de graficas: una que ofrece la magnitud |G(j!)| contra la frecuencia y la otra que muestra el ´Angulo de fase _(j!) contra la frecuencia. Un ejemplo de la raza de bode se muestra en la figura

El eje de abscisas es logarítmico en!, es decir, lineal en log(!), donde el logaritmo es de base 10. así se consigue una representación compacta sobre un rango amplio de frecuencias. La unidad del eje es la década, es decir, la distancia entre ! y 10! para cualquier valor de !. La magnitud de la respuesta en frecuencia se mide en decibeles [dB], es decir, unidades de 20 log (!) La fase se mide en escala lineal en radianes o grados.

ACCIONES BASICAS DE CONTROL

Empezaremos con una clasificación de los diferentes controladores industrial:

1. De dos posiciones o de encendido y apagado (on-off)

2. Proporcionales

3. Integrales

4. Proporcionales-Integrales

5. Proporcionales-Derivativos

6. Proporcionales-Integrales-Derivativos

5.1 Acción de Control Proporcional Se basa en la relación entre la señal de salida del controlador u(t) y la señal de error e(t).

o su equivalente en función de transferencia se obtiene aplicando transformada de Laplace

Donde:

Kp se considera la ganancia proporcional. Este tipo de controlador puede ser visto como un amplificador con una ganancia ajustable, su representación es la mostrada en la figura

Acción de Control Integral

El valor de la salida del controlador u(t) se cambia a una razón proporcional a la señal de

error e(t), es decir:

O bien:

donde:

Ki es una constante ajustable su equivalente en función de transferencia es:

Si se duplica el valor de e(t) el valor de u(t) varia dos veces mas rápido, cuando e(t) = 0, el valor de u(t) permanece estacionario es decir se mantiene el valor de la entrada del proceso. En ocasiones este es denominado también control de reajuste (reset); su representación en diagrama de bloques es el representado en la figura

Acción de Control Proporcional-Integral

La acción de este controlador se define mediante:

o su equivalente en función de transferencia:

Ambos parámetros son ajustables, el tiempo integral ajusta la acción de control integral, mientras que un cambio en el valor de la ganancia proporcional, afecta las partes integral y proporcional de la acción de control. El inverso de Ti se denomina velocidad de reajuste, esta indica la cantidad de veces por minuto que se duplica la parte proporcional de la acción de control; su representación en diagrama de bloques es el mostrado en la figura. la respuesta ante una entrada escalón de un controlador PI

Efectos del Control Proporcional-Integral

La aplicación de este tipo de control produce los siguientes efectos sobre sistema a controlar:

Respuesta a entrada escalón de un Controlador Proporcional-Integral

· Mejora el amortiguamiento y reduce el sobre paso máximo

· Incrementa el tiempo de levantamiento

· Disminuye el ancho de banda

· Mejora el margen de ganancia y de fase y la magnitud de pico de resonancia

· Filtra el ruido a alta frecuencia

· El error en estado estable se mejora con un orden es decir, si el error en estado estable a una entrada dada es constante, el control PI lo reduce a cero.

Este tipo de controlador se utiliza generalmente cuando se desea mejorar el error en estado estacionario. Los sistemas se hacen normalmente mas oscilatorios, si no se ajusta correctamente se puede hacer inestable.

Acción de Control Proporcional-Derivativa

Esta acción de control se define mediante:

Su representación en diagrama de bloques es la mostrada en la figura

señal de salida de este tipo de acción, también llamada Control de Velocidad, es proporcional a la velocidad de cambio de la señal de error. La constante es el intervalo de tiempo durante el cual la acción de la velocidad hace avanzar el efecto de la acción proporcional. La respuesta ante una entrada escalón de un controlador PD se muestra en la figura

Efectos del Control Proporcional-Derivativo

La aplicación de este tipo de control produce los siguientes efectos sobre sistema a controlar:

· Mejora el amortiguamiento y reduce el sobrepaso máximo

· Reduce el tiempo de levantamiento y el tiempo de asentamiento

· Incrementa el ancho de banda

· Mejora el margen de ganancia y de fase y la magnitud de pico de resonancia

· Puede acentuar el ruido en altas frecuencias

· No es efectivo para sistemas ligeramente amortiguados o inicialmente estables

· El error en régimen permanente no es afectado a menos que se varié con el tiempo

Acción de Control Proporcional-Integral-Derivativa

Esta acción combinada tiene las ventajas y efectos de las acciones de control PD y PI, su

Ecuación viene dada por:

Su función de transferencia es:

Donde:

Kp= Ganancia Proporcional

Ti= Tiempo Integral

Td= Tiempo Derivativo

su representación en diagrama de bloques es la mostrada en la figura

La respuesta ante una entrada escalón de un controlador PID ideal se muestra en la figura

CONTROL PID CLASICO

La familia de controladores de estructura fija o controladores PID, han mostrado ser robustos y extremadamente beneficiosos en el control de muchas aplicaciones de importancia en la industria

siendo el más ampliamente utilizado en la industria moderna, controlando más del 95 porciento de los procesos industriales en lazo cerrado.

Estructura de un PID

Para representar la estructura de un controlador PID se considera un lazo básico de control SISO (única entrada, única salida) el cual se presenta en la figura

REGLAS DE SINTONIZACI ON PARA CONTROLADORES PID

El proceso de seleccionar los parámetros del controlador que cumplan con las especificaciones de desempeño se conoce como sintonización del controlador. Es posible aplicar diversas técnicas de diseño con el fin de determinar los parámetros del controlador que cumpla las especificaciones en estado transitorio y en estado estable del sistema en lazo cerrado. Ziegler y Nichols sugirieron reglas para sintonizar los controladores PID lo cual significa establecer valores Kp, Ti, Td; basados en la respuestas escalón experimentales o en valor de Kp que se produce en estabilidad marginal cuando solo se usa la acción de control proporcional. A continuación se presentan las reglas Ziegler- Nichols, las cuales son muy convenientes cuando no se conocen los modelos matemáticos de las plantas.

EJEMLPO

La curva de respuesta en lazo abierto de un sistema de control de temperatura de tope de una columna que separa la mezcla etanol-agua es la que se muestra en la figura.

La principal perturbación son los cambios en la composición de la corriente de alimentación, cuya dinámica puede considerarse idéntica a la de los elementos del lazo, salvo que su ganancia vale 1.56 (%/% de composición)

· Sintonice un controlador PI empleando el método de Ziegler y Nichols en lazo abierto

· Compare empleando índices de conducta apropiados cuánto mejoraría la respuesta si se adiciona acción derivativa al controlador. Considere como perturbación un escalón de magnitud uno en la composición de alimentación.

Sintonización de controladores

El método de Ziegler y Nichols que emplea la curva de respuesta como información para la sintonización, asimila la el comportamiento del lazo de una forma simplificada con una constante de tiempo y tiempo muerto.